Определение максимального объема коробки
I этап. Постановка задачи
Описание задачи
Имеется квадратный лист картона со стороной а. Из листа делают коробку следующим образом: по углам вырезают четыре квадрата и склеивают коробку по сторонам вырезов.
Цель моделирования
Определить, какова должна быть сторона вырезаемого квадрата, чтобы коробка имела наибольшую вместимость.
Анализ объекта
В задаче рассматривается процесс преобразования одного объекта (картонного листа) в другой (коробку). Исходный объект – картонный лист – имеет заданные геометрические размеры: длина стороны а. Созданный объект – коробка – характеризуется объемом, а вырезы – размером стороны и площадью.
II этап. Разработка модели
Информационная модель
|
Объект “картонный лист” |
|
|
управляемые параметры |
действия над объектом |
|
Длина стороны а |
Вырезание квадратных областей по краям |
|
Длина выреза b |
Склеивание сторон вырезов |
|
Объект “коробка” |
|
|
управляемые параметры |
действия над объектом |
|
Длина стороны c |
Расчет площади и объема |
|
Площадь дна S |
|
|
Объем V |
|
Геометрическая модель
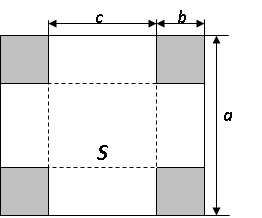
Математическая модель
Расчетные формулы:
- c = a – 2b - длина стороны дна;
- S = c2 – площадь дна;
- V = Sb – объем.
Здесь a – длина стороны картонного листа, b – длина выреза.
Компьютерная модель
Для моделирования используем среду электронной таблицы, в которой информационная и математическая модели объединяются в таблицу, которая имеет три области:
- исходные данные - управляемые параметры;
- промежуточные расчеты;
- результаты.
Задание
Заполните область исходных данных по предложенному образцу, при этом составьте таблицу расчета со столбцами “Длина выреза”, “Длина стороны”, “Площадь дна”, “Объем”. Длину выреза изменяйте с шагом 1 см. Заметьте, что для различных значений исходного размера картонного листа понадобиться разное количество расчетных строк в таблице. (Образец)
III этап. Компьютерный эксперимент
План моделирования
- Провести тестовый расчет компьютерной модели по данным, приведенным в таблице.
- Провести расчеты для различных исходных данных (длина стороны картонного листа).
- Провести расчеты с более мелким шагом увеличения выреза (например, 0,5 см).
- Провести анализ модели.
Технология моделирования
- Определите по столбцу “Объем” наибольший объем коробки (с помощью встроенной функции МАКС).
- В столбце “Длина выреза” определите значение выреза, соответствующее наибольшему объему коробки.
- Составьте таблицу результатов расчета для различных значений исходного размера картонного листа.
IV этап. Анализ результатов моделирования
Ответьте на следующие вопросы:
- По столбцу “Длина стороны” определяем, что длина стороны коробки все время уменьшается, пока не станет равной 0. Если заполнено большее количество строк, то их длина стороны уже меньше 0. Чем это можно объяснить? Надо ли эти строки учитывать при определении максимального объема?
- Как изменяется оптимальный размер выреза, если изменять шаг выреза? Чем это можно объяснить?
|
Задача о склеивании коробки |
|||
|
|
|
|
|
|
Исходные данные |
|
|
|
|
Длина стороны |
40 |
|
|
|
Шаг увеличения выреза |
1 |
|
|
|
Расчет |
|||
|
Промежуточные расчеты |
Результаты |
||
|
Длина выреза b |
Длина стороны a |
Площадь дна S |
Объем V |
|
1 |
38 |
1444 |
1444 |
|
2 |
36 |
1296 |
2592 |
|
3 |
34 |
1156 |
3468 |
|
4 |
32 |
1024 |
4096 |
|
5 |
30 |
900 |
4500 |
|
6 |
28 |
784 |
4704 |
|
7 |
26 |
676 |
4732 |
|
8 |
24 |
576 |
4608 |
|
9 |
22 |
484 |
4356 |
|
10 |
20 |
400 |
4000 |
|
11 |
18 |
324 |
3564 |
|
12 |
16 |
256 |
3072 |
|
13 |
14 |
196 |
2548 |
|
14 |
12 |
144 |
2016 |
|
15 |
10 |
100 |
1500 |
|
16 |
8 |
64 |
1024 |
|
17 |
6 |
36 |
612 |
|
18 |
4 |
16 |
288 |
|
19 |
2 |
4 |
76 |
|
20 |
0 |
0 |
0 |





